مقناطیسی سرکٹس کا حساب

برقی مشینوں اور آلات میں، مقناطیسی بہاؤ F مقناطیسی سرکٹ (فیرو میگنیٹک کور) اور اس مقناطیسی سرکٹ کے ہوا کے خلاء میں مرتکز ہوتا ہے۔ مقناطیسی بہاؤ کے اس راستے کو مقناطیسی سرکٹ کہا جاتا ہے۔

مقناطیسی سرکٹ ایک برقی سرکٹ کی طرح ہوتا ہے۔ مقناطیسی بہاؤ Ф ایک برقی کرنٹ I سے مشابہت رکھتا ہے، انڈکشن В کرنٹ کی کثافت سے مشابہت رکھتا ہے، مقناطیسی قوت (ns) Fн (H ∙ l = I ∙ ω) e کے مساوی ہے۔ وغیرہ کے ساتھ

سادہ ترین صورت میں، مقناطیسی سرکٹ کا ہر جگہ ایک ہی کراس سیکشن ہوتا ہے اور یہ ایک یکساں مقناطیسی مواد سے بنا ہوتا ہے۔ تعین کرنا n. l ∙ ω کے ساتھ مطلوبہ انڈکشن B فراہم کرنے کے لیے، متعلقہ شدت H کا تعین مقناطیسی وکر سے کیا جاتا ہے اور مقناطیسی فیلڈ لائن کی اوسط لمبائی سے ضرب کیا جاتا ہے l: H ∙ l = I ∙ ω = Fm۔

یہاں سے، مطلوبہ کرنٹ I یا کنڈلی کے موڑوں کی تعداد ω کا تعین کیا جاتا ہے۔

ایک پیچیدہ مقناطیسی سرکٹ میں عام طور پر مختلف حصوں اور مقناطیسی مواد کے ساتھ حصے ہوتے ہیں۔ یہ حصے عام طور پر سیریز میں جڑے ہوتے ہیں، اس لیے ایک ہی مقناطیسی بہاؤ F ان میں سے ہر ایک سے گزرتا ہے۔ہر سیکشن میں انڈکشن B کا انحصار سیکشن کے کراس سیکشن پر ہوتا ہے اور ہر سیکشن کے لیے الگ الگ فارمولہ B = Φ∶S کے ذریعے شمار کیا جاتا ہے۔

انڈکشن کی مختلف اقدار کے لیے، شدت H کا تعین میگنیٹائزیشن وکر سے کیا جاتا ہے اور اسے سرکٹ کے متعلقہ حصے کی پاور لائن کی اوسط لمبائی سے ضرب دیا جاتا ہے۔ انفرادی کاموں کا خلاصہ کرتے ہوئے، کسی کو مکمل ن مل جاتا ہے۔ c. مقناطیسی سرکٹ:

Fm = I ∙ ω = H1 ∙ l1 + H2 ∙ l2 + H3 ∙ l3 + … جو مقناطیسی کرنٹ یا کنڈلی کے موڑ کی تعداد کا تعین کرتا ہے۔

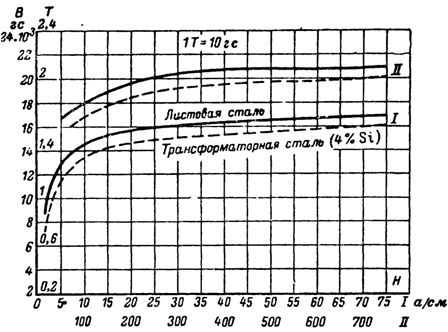
مقناطیسی منحنی خطوط

کی مثالیں

1. 200 موڑ والے کوائل کا مقناطیسی کرنٹ I کیا ہونا چاہیے تاکہ n۔ c. کاسٹ آئرن کی انگوٹھی میں مقناطیسی بہاؤ پیدا کیا گیا Ф = 15700 Ms = 0.000157 Wb؟ کاسٹ آئرن کی انگوٹھی کا اوسط رداس r = 5 سینٹی میٹر ہے، اور اس کے حصے کا قطر d = 2 سینٹی میٹر ہے (تصویر 1)۔

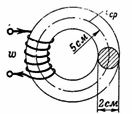
چاول۔ 1۔

مقناطیسی سرکٹ کا سیکشن S = (π ∙ d^2) / 4 = 3.14 cm2۔

کور میں شامل کرنا ہے: B = Φ∶S = 15700∶ 3.14 = 5000 G۔

MKSA سسٹم میں، انڈکشن ہے: B = 0.000157 Wb: 0.0000314 m2 = 0.5 T۔

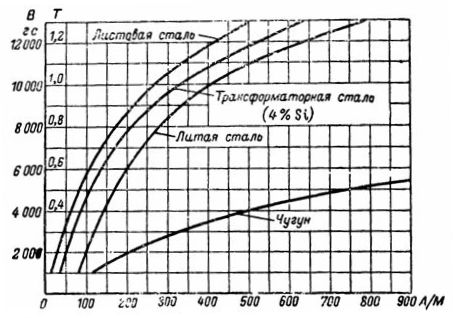
کاسٹ آئرن کے میگنیٹائزیشن وکر سے، ہمیں B = 5000 G = 0.5 T کے لیے مطلوبہ طاقت H 750 A/m کے برابر ہے۔ میگنیٹائزیشن کی طاقت اس کے برابر ہے: I ∙ ω = H ∙ l = 235.5 Av۔

لہذا، مطلوبہ کرنٹ I = (H ∙ l) / ω = 235.5 / 200 = 1.17 A۔

2. ایک بند مقناطیسی سرکٹ (تصویر 2) ایک ٹرانسفارمر کی سٹیل پلیٹوں سے بنا ہے۔ کور Ф = 160000 Ms = 0.0016 Wb میں مقناطیسی بہاؤ بنانے کے لیے 0.5 A کے کرنٹ کے ساتھ کوائل میں کتنے موڑ ہونے چاہئیں؟

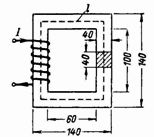
چاول۔ 2.

کور سیکشن S = 4 ∙ 4 = 16 cm2 = 0.0016 m2۔

کور انڈکشن B = F/S = 160000/16 = 10000 Gs = 1 T۔

ٹرانسفارمر سٹیل کے میگنیٹائزیشن وکر کے مطابق، ہم B = 10,000 Gs = 1 T کی شدت H = 3.25 A/cm = 325 A/m تلاش کرتے ہیں۔

مقناطیسی فیلڈ لائن کی اوسط لمبائی l = 2 ∙ (60 + 40) + 2 ∙ (100 + 40) = 480 = 0.48 میٹر ہے۔

مقناطیسی قوت Fm = I ∙ ω = H ∙ l = 3.25 ∙ 48 = 315 ∙ 0.48 = 156 Av۔

0.5 A کے کرنٹ پر، موڑ کی تعداد ω = 156 / 0.5 = 312 ہے۔

3. انجیر میں دکھایا گیا مقناطیسی سرکٹ۔ 3 پچھلی مثال کے مقناطیسی سرکٹ کی طرح ہے، سوائے اس کے کہ اس میں δ = 5 ملی میٹر کا ہوا کا فرق ہے۔ کیا ہونا چاہیے؟ s. اور کوائل کرنٹ تاکہ مقناطیسی بہاؤ پچھلی مثال کی طرح ہو، یعنی F = 160000 Ms = 0.0016 Wb؟

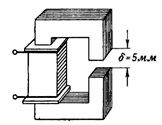
چاول۔ 3.

مقناطیسی سرکٹ میں دو سلسلے سے منسلک حصے ہوتے ہیں، جن کا کراس سیکشن پچھلی مثال کی طرح ہی ہے، یعنی S = 16 cm2۔ انڈکٹنس بھی B = 10000 G = 1 T کے برابر ہے۔

سٹیل کی مقناطیسی لائن کی اوسط لمبائی تھوڑی چھوٹی ہے: lс = 48-0.5 = 47.5 سینٹی میٹر ≈0.48 میٹر۔

مقناطیسی سرکٹ کے اس حصے میں مقناطیسی وولٹیج Hc ∙ lc = 3.25 ∙ 48≈156 Av ہے۔

ایئر گیپ میں فیلڈ کی طاقت ہے: Hδ = 0.8 ∙ B = 0.8 ∙ 10000 = 8000 A/cm۔

ایئر گیپ کے کراس سیکشن میں مقناطیسی تناؤ Hδ ∙ δ = 8000 ∙ 0.5 = 4000 Av۔

مکمل n. c. انفرادی حصوں میں مقناطیسی وولٹیج کے مجموعہ کے برابر ہے: I ∙ ω = Hс ∙ lс + Hδ ∙ δ = 156 + 4000 = 4156 Av۔ I = (I ∙ ω) / ω = 4156/312 = 13.3 A۔

اگر پچھلی مثال میں مطلوبہ مقناطیسی بہاؤ 0.5 A کے کرنٹ کے ذریعے فراہم کیا گیا تھا، تو پھر 0.5 سینٹی میٹر کے ہوا کے فرق کے ساتھ مقناطیسی سرکٹ کے لیے اسی مقناطیسی بہاؤ کو حاصل کرنے کے لیے 13 A کا کرنٹ درکار ہے۔ اس سے یہ دیکھا جا سکتا ہے کہ مقناطیسی سرکٹ کی لمبائی کے سلسلے میں ایک ہوا کا فرق، مطلوبہ n کو بہت زیادہ بڑھاتا ہے۔ v. اور کوائل کرنٹ۔

4. ٹرانسفارمر کا مقناطیسی بہاؤ F = 72000 Ms کے حساب سے لگایا جاتا ہے۔ n کا حساب درکار ہے۔s.اور پرائمری وائنڈنگ کا مقناطیسی کرنٹ جس میں 800 موڑ ہوتے ہیں۔ ٹرانسفارمر کے کور میں ایک فرق δ = 0.2 ملی میٹر ہے۔ ٹرانسفارمر کور کے طول و عرض کو انجیر میں دکھایا گیا ہے۔ 4. کور کا کراس سیکشن S = 2 ∙ 3 ​​​ = 6 cm2 (اس شکل کے کور والے ٹرانسفارمرز کو آرمرڈ کہا جاتا ہے)۔

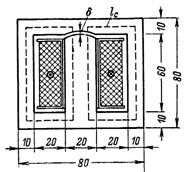
چاول۔ 4.

کور اور ایئر گیپ انڈکشن B = F/S = 72000/6 = 12000 G۔

B = 12000 G کے لیے ٹرانسفارمر اسٹیل کے میگنیٹائزیشن وکر کے مطابق، ہم شدت کا تعین کرتے ہیں: Hc = 5 A/cm۔

سٹیل میں مقناطیسی لکیر کی اوسط لمبائی lс = 2 ∙ (6 + 3) = 18 سینٹی میٹر ہے۔

ایئر گیپ میں وولٹیج Hδ = 0.8 ∙ B = 9600 A/cm۔

مقناطیسی قوت I ∙ ω = Hc ∙ lc + Hδ ∙ δ = 5 ∙ 18 + 9600 ∙ 0.02 = 90 + 192 = 282 Av; I = (I ∙ ω) / ω = 282/800 = 0.35 A۔

آرمرڈ کور میں، مقناطیسی بہاؤ دو حصوں میں تقسیم ہو جاتا ہے، جو سائیڈ راڈز کے ساتھ بند ہوتے ہیں، جس کا کراس سیکشن S/2 ہے، اور مقناطیسی لائن کی اوسط لمبائی lc ہے۔ نتیجے کے طور پر، مقناطیسی سرکٹ ایک عام کور S اور پاور لائن lc کی لمبائی والے روایتی ٹرانسفارمر کے مقناطیسی سرکٹ سے مکمل طور پر مشابہ ہے۔

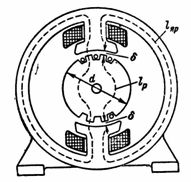
5. DC مشین کا مقناطیسی بہاؤ F = 1280000 Mks۔ مقناطیسی سرکٹ میں ایک کاسٹ اسٹیل کا جوا ہوتا ہے جس کی اوسط مقناطیسی لائن کی لمبائی lа = 80 سینٹی میٹر ہوتی ہے، ایک روٹر جو الیکٹرک اسٹیل پلیٹوں سے اسمبل ہوتا ہے جس کی اوسط فیلڈ لمبائی lр = 18 سینٹی میٹر ہوتی ہے، اور ہر ایک میں دو ایئر گیپس 0.2 سینٹی میٹر ہوتے ہیں۔ = 8 ∙ 20 cm2; روٹر اور پول سیکشن Sр = 12 ∙ 20 cm2... حساب لگائیں n۔ p. اور قطب کنڈلی کے موڑوں کی تعداد، اگر اس میں زیادہ سے زیادہ مقناطیسی (پرجوش) کرنٹ 1 A ہے (تصویر 5)۔

چاول۔ 5۔

جوئے اور قطب میں شامل کرنا Bя = Ф / Sя = 1280000/160 = 8000 G۔

Bя = 8000 G پر کاسٹ اسٹیل کے مقناطیسی وکر کے مطابق جوئے اور قطب میں وولٹیج اس کے برابر ہے:

H = 2.8 A / cm.

جوئے کے حصے میں مقناطیسیت کی قوت HЯ ∙ la = 2.8 ∙ 80 = 224 Av۔

روٹر، پول اور ایئر گیپ میں انڈکشن Br = Ф / Ср = 1280000/240 = 5333 G.

اسٹیل پلیٹوں سے بنے روٹر میں وولٹیج Br = 5333 Gs Hrp = 0.9 A/cm،

اور روٹر سیکشن کا مقناطیسی وولٹیج Hр ∙ lр = 0.9 ∙ 18 = 16.2 Av۔

ایئر گیپ میں وولٹیج Hδ = 0.8 ∙ Bδ = 0.8 ∙ 5333 = 4266.4 A/cm۔

ایئر گیپ کے کراس سیکشن میں مقناطیسی وولٹیج Hδ ∙ 2 ∙ δ = 4266.4 ∙ 2 ∙ 0.2 = 1706.56 A۔

مکمل n. c. الگ الگ حصوں میں مقناطیسی وولٹیج کے مجموعے کے برابر: I ∙ ω = Hя ∙ la + Hр ∙ lр + Hδ ∙ 2 ∙ δ; I ∙ ω = 224 + 16.2 + 1706.56 = 1946.76 Av۔

دو قطبی کنڈلیوں میں موڑ کی تعداد ω = (I ∙ ω) / I = 1946.76 / 1≈2000۔