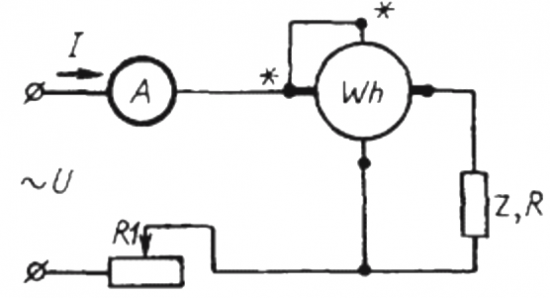
الٹرنیٹنگ کرنٹ سرکٹ میں پاور فیکٹر کے بالواسطہ تعین کے اصول اور طریقے

پاور فیکٹر یا کوسائن فائیسائنوسائیڈل الٹرنیٹنگ کرنٹ کے استعمال کنندہ کے حوالے سے، نیٹ ورک سے اس صارف کو فراہم کی جانے والی کل پاور S اور فعال بجلی کی کھپت P کا تناسب ہے۔

کل طاقت S، عام صورت میں، موجودہ I اور زیر غور سرکٹ میں وولٹیج U کی مؤثر (جڑ کا مطلب مربع) اقدار کی پیداوار کے طور پر بیان کیا جا سکتا ہے، اور ایکٹو پاور P — جیسا کہ صارف کے ذریعے ناقابل واپسی طور پر استعمال کیا جاتا ہے۔ کام کا آپریشن.

رد عمل کی طاقت Qاگرچہ یہ کل طاقت کا حصہ ہے، تاہم، یہ کام کرنے کے لیے استعمال نہیں کیا جاتا، بلکہ صارف کے سرکٹ کے کچھ عناصر میں صرف متبادل برقی اور مقناطیسی شعبوں کی تخلیق میں حصہ لیتا ہے۔

سوائے براہ راست طاقت عنصر کی پیمائش الیکٹروڈینامک آلات کا استعمال - فیز میٹر, کافی منطقی بالواسطہ طریقے ہیں جو آپ کو اس انتہائی اہم برقی مقدار کی قدر کو ریاضی کے لحاظ سے درست طریقے سے سمجھنے کی اجازت دیتے ہیں جو صارف کو سائنوسائیڈل الٹرنیٹنگ کرنٹ سرکٹ میں نمایاں کرتی ہے۔

آئیے ڈیٹا کو دیکھتے ہیں۔ بالواسطہ طریقے تفصیل سے، آئیے بالواسطہ طاقت کے عنصر کی پیمائش کے اصول کو سمجھیں۔

وولٹ میٹر، امیٹر اور واٹ میٹر کا طریقہ

الیکٹروڈینامک واٹ میٹر اس کی حرکت پذیر کنڈلی کے سرکٹ میں اضافی فعال مزاحمت کے ساتھ AC سرکٹ P میں استعمال ہونے والی انتہائی فعال طاقت کی قدر کی نشاندہی کرتا ہے۔

اگر اب، ایک وولٹ میٹر اور ایک ایمیٹر کا استعمال کرتے ہوئے، ہم زیر مطالعہ لوڈ کے سرکٹ میں کام کرنے والے موجودہ I اور وولٹیج U کی اوسط قدروں کی پیمائش کرتے ہیں، تو ان دو پیرامیٹرز کو ضرب کرنے سے، ہمیں صرف کل پاور S ملے گی۔ .

پھر کسی دیے گئے بوجھ کا پاور فیکٹر (کوزائن فائی) فارمولے کا استعمال کرتے ہوئے آسانی سے پایا جا سکتا ہے:

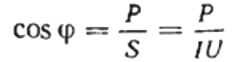
یہاں، اگر آپ چاہیں تو، آپ ری ایکٹیو پاور Q کی قدر بھی تلاش کر سکتے ہیں، سرکٹ z کی کل مزاحمت اوہ کے قانون، نیز فعال اور رد عمل مزاحمت، محض ایک مزاحمتی مثلث بنا کر یا اس کی نمائندگی کرتے ہوئے، اور پھر پائتھاگورین تھیوریم کا استعمال کرتے ہوئے:

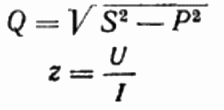
کاؤنٹر اور ایممیٹر کا طریقہ

اس طریقہ کو استعمال کرنے کے لیے، ایک سرکٹ کو جمع کرنا ضروری ہے جس میں سب سے آسان کو لوڈ Z اور ammeter کے ساتھ سیریز میں جوڑا گیا ہو۔ بجلی کا میٹر ک

وقت کی ایک مخصوص مدت کے لیے، ایک منٹ کی ترتیب کے مطابق، ڈسک N کے گردشوں کی تعداد کا حساب لگانا ضروری ہو گا، جو ایک مقررہ وقت کے دوران خرچ ہونے والی فعال توانائی کی مقدار کو ظاہر کرے گا (یعنی، کو مدنظر رکھتے ہوئے پاور فیکٹر).

یہاں: ڈسک N کے ریوولیشنز کی تعداد، گتانک k فی انقلاب توانائی کی مقدار ہے، I اور U بالترتیب rms کرنٹ اور وولٹیج ہیں، t انقلابات کو شمار کرنے کا وقت ہے، cosine phi پاور فیکٹر ہے:

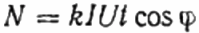
پھر، مطالعہ شدہ صارف Z کے بجائے، فعال لوڈ R کو اسی کاؤنٹر کے ذریعے سرکٹ میں شامل کیا جاتا ہے، لیکن براہ راست نہیں، بلکہ rheostat R1 کے ذریعے (وہی کرنٹ I حاصل کرنا، جیسا کہ پہلی صورت میں، صارف Z کے ساتھ)۔ ڈسک N1 کے انقلابات کی تعداد اسی وقت کے لئے برقرار رکھی جاتی ہے۔ لیکن یہاں، چونکہ لوڈ فعال ہے، کوزائن فائی (پاور فیکٹر) یقینی طور پر 1 کے برابر ہے۔ اس لیے:

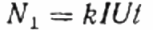
پھر ڈسک کاؤنٹر کے انقلابات کا تناسب پہلی اور دوسری صورتوں میں ایک ہی مدت کے لیے ریکارڈ کیا جاتا ہے۔ یہ cosine phi ہو گا، یعنی پہلے لوڈ کا پاور فیکٹر (خالص طور پر ایکٹو لوڈ کے ساتھ نسبت موجودہ):

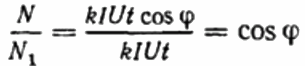
تین ammeter طریقہ

تین ایمیٹرز کا استعمال کرتے ہوئے سائنوسائیڈل کرنٹ سرکٹ میں پاور فیکٹر کا تعین کرنے کے لیے، آپ کو پہلے درج ذیل سرکٹ کو جمع کرنا ہوگا۔

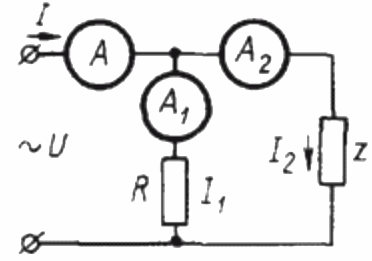
یہاں Z ایک بوجھ ہے جس کے پاور فیکٹر کا تعین کیا جانا ہے اور R خالص طور پر ایکٹو لوڈ ہے۔

چونکہ لوڈ R خالصتاً فعال ہے، اس لیے کسی بھی لمحے موجودہ I1 اس بوجھ پر لگائے گئے متبادل وولٹیج U کے ساتھ مرحلے میں ہے۔ اس صورت میں، کرنٹ I کرنٹ I1 اور I2 کے ہندسی جمع کے برابر ہے۔ اب ہم اس پوزیشن کی بنیاد پر کرنٹ کا ایک ویکٹر ڈایاگرام بنائیں گے۔

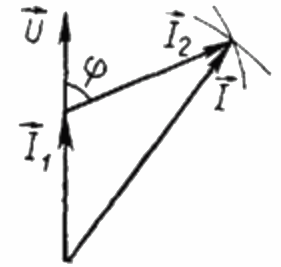
کرنٹ کے ویکٹر ڈایاگرام پر، موجودہ I1 اور موجودہ I2 کے درمیان شدید زاویہ زاویہ phi ہے، جس کا کوسائن (حقیقت میں، پاور فیکٹر کی قدر) قدروں کی ایک خاص جدول سے تلاش کیا جا سکتا ہے۔ مثلثی افعال کا یا فارمولے سے حساب کیا جاتا ہے:

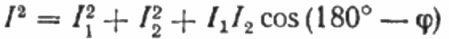
یہاں سے ہم cosine phi کا اظہار کر سکتے ہیں، یعنی مطلوبہ پاور فیکٹر:

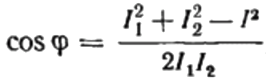
پائے جانے والے پاور فیکٹر کا نشان («+» یا «-«) بوجھ کی نوعیت کی نشاندہی کرے گا۔ اگر پاور فیکٹر (کوزائن فائی) منفی ہے، تو بوجھ فطرت میں کیپسیٹو ہے۔ اگر پاور فیکٹر ایک مثبت قدر ہے، تو بوجھ کی نوعیت انڈکٹیو ہے۔